❅ Contoh 1 ❅
Harga 4 buah permen A dan 3 buah permen B adalah Rp2.500,00, sedangkan harga 2 buah permen A dan 7 buah permen B adalah Rp2.900,00. Berapakah harga 2 lusin permen A dan 4 lusin permen B?
✍ Penyelesaian:
Mula-mula kita harus membuat 2 buah persamaan linear dari informasi yang diketahui pada soal.
Misalkan:
harga 1 buah permen A = x
harga 1 buah permen B = y
Kalimat “Harga 4 buah permen A dan 3 buah permen B adalah Rp2.500,00” diubah menjadi,
…. Persamaan (1)Kalimat “Harga 2 buah permen A dan 7 buah permen B adalah Rp2.900,00” diubah menjadi,
…. Persamaan (2)
Sekarang kita sudah mempunyai 2 persamaan linear. Selanjutnya kita tinggal menyelesaikan SPLDV tersebut dengan menggunakan salah satu metode.
Pada contoh ini kita akan menggunakan metode eliminasi.
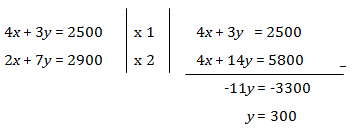
Kemudian, nilai y = 300 kita substitusikan ke salah satu persamaan
4x+3y4x+3(300)4x+9004xx=2500=2500=2500=400
Diperoleh:
harga permen A = Rp400,00
harga permen B = Rp300,00
1 lusin = 12 buah
Harga 2 lusin permen A =
Harga 4 lusin permen B =
Jadi, harga 2 lusin permen A dan 4 lusin permen B adalah Rp9.600,00 dan Rp14.400,00.
❅ Contoh 2 ❅
Umur Sani 7 tahun lebih tua dari umur Ari, sedangkan jumlah umur mereka adalah 43 tahun. Berapakah umur mereka masing-masing ?
✍ Penyelesaian:
Mula-mula kita harus membuat 2 buah persamaan linear dari apa yang diketahui pada soal.
Misalkan:
umur Sani = x
umur Ari = y
Kalimat “Umur Sani 7 tahun lebih tua dari umur Ari” diubah menjadi:
…. Persamaan (1)
Kalimat “Jumlah umur mereka adalah 43 tahun” diubah menjadi:
…. Persamaan (2)
Sekarang kita sudah mempunyai 2 persamaan linear. Selanjutnya kita tinggal menyelesaikan SPLDV tersebut dengan menggunakan salah satu metode.
Pada contoh ini kita akan menggunakan teknik substitusi.
Substitusikan nilai x pada persamaan (1) ke persamaan (2), sehingga diperoleh:
Kemudian, kita substitusikan nilai y ke salah satu persamaan:
Jadi, umur Sani 25 tahun dan umur Ari 18 tahun.





0 comments:
Post a Comment