Persamaan Garis Lurus

KONSEP GRADIEN DAN GARIS LURUS

Dalam aktivitas sehari-hari, tentunya kalian pernah menggambar garis lurus, namun apakah kalian tahu bahwa setiap garis lurus mempunyai kemiringan tertentu?

Mari kita cermati gambar ruas jalan berikut ini.

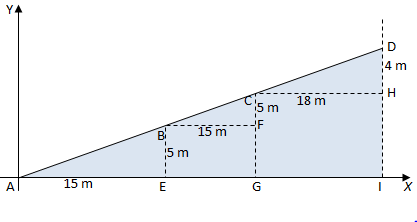
Ruas jalan dari A sampai D posisi jalannya miring. Pada ruas jalan dari A sampai B, jarak horizontalnya 15 m dan ketinggiannya 5 m, sedangkan pada ruas jalan dari C sampai D, jarak horizontalnya 18 m dan ketinggiannya 4 m.

Pengertian Gradien

Ukuran kemiringan, yang selanjutnya disebut gradien, untuk masing-masing ruas garis pada gambar di atas dapat ditentukan dengan cara berikut.

1. AE, BF, AG, dan CH merupakan perubahan jarak mendatar yang selanjutnya disebut dengan perubahan nilai x atau perubahan jarak mendatar.
2. BE, CF, CG, dan DH merupakan perubahan jarak tegak yang selanjutnya disebut dengan perubahan nilai y atau perubahan jarak tegak.

Dengan kata lain, gradien merupakan nilai perbandingan antara perubahan nilai y dengan perubahan nilai x.

Perhatikan gradien ruas garis AB, BC, dan AC pada uraian di atas. Ternyata ketiga ruas garis tersebut memiliki gradien yang sama, yaitu 1/3 , walaupun panjangnya berbeda.

Jadi, gradien garis tidak tergantung pada panjang garis.

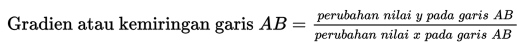
Gradien Garis pada Bidang Koordinat Cartesius

Perhatikan gambar di bawah ini.

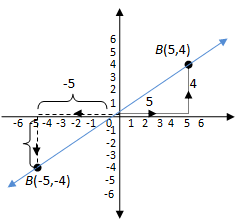
Pada garis k , terdapat ruas garis OA dan OB dengan koordinat O(0 , 0), A(5 , 4), dan B(-5 , -4).

Dengan demikian,

Jadi, gadien garis k = gradien OA = gradien OB = 4/5

Berdasarkan uraian di atas, dapat ditarik kesimpulan sebagai berikut :

1. Untuk menentukan gradien garis k, kita perlu memilih salah satu ruas garis pada garis k, misal : garis OA atau OB.
2. Perubahan nilai x bernilai positif jika bergerak ke kanan (dari O bergerak ke C)
3. Perubahan nilai x bernilai negatif jika bergerak ke kiri (dari O bergerak ke D)
4. Perubahan nilai y bernilai positif jika bergerak ke atas (dari C bergerak ke A)
5. Perubahan nilai y bernilai negatif jika bergerak ke bawah (dari D bergerak ke B)
6. Garis dengan kemiringan seperti garis k mempunyai gradien bernilai positif

Gradien Garis yang Melalui Dua Titik

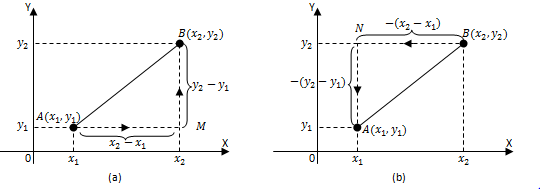
Perhatikan titik A(x1 , y1) dan B(x2 , y2) pada gambar di atas.

Untuk menentukan gradien garis AB pada gambar (a), terlebih dahulu kita tentukan perubahan nilai x dan perubahan nilai y dari garis AB.

1. Perubahan nilai x garis AB = AM = x2 - x1
2. Perubahan nilai y garis AB = MB = y2 - y1

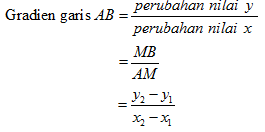
Untuk selanjutnya, gradien garis AB dapat ditulis mAB

Gradien Garis yang saling Sejajar

Garis-garis yang sejajar memiliki gradien yang sama.
m1 = m2

Gradien Garis yang saling Tegak Lurus

Hasil kali gradien antara kedua garis yang saling tegak lurus adalah (-1)
m1 X m2 = - 1

Garis Lurus

Bentuk umum dari persamaan garis lurus adalah y = mx + c atau ax + by = c

Selanjutnya, 
1. gradien dari garis y = mx + c adalah m 
2. gradien dari garis ax + by = c adalah -a/b

Aksioma : melalui dua buah titik hanya dapat dibuat sebuah garis lurus.

Dengan demikian, hanya ada satu garis yang melalui titik (x1 , y1) dan (x2 , y2) , yaitu :

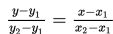
Untuk memperdalam pemahaman kalian, mari kita mencermati beberapa contoh soal berikut ini.

Contoh 1 :

Gambar di bawah menunjukkan tampak samping dari bagian tangga beton. Hitunglah gradien tangga tersebut!

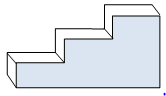
Penyelesaian :

Untuk menentukan gradien, kita perlu membuat garis yang melalui pojok-pojok atas tangga seperti gambar di bawah.

Contoh 2 :

Tentukan gradien garis yang menghubungkan pasangan titik P(- 3, 6) dan Q(5, - 4).

Penyelesaian :

1. Karena P(-3 , 6) maka x1 = -3 dan y1 = 6
2. Karena P(5 , -4) maka x1 = 5 dan y1 = -4

Dengan demikian,

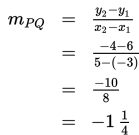
Contoh 3 :

Garis g yang bergradien -5/3 sejajar dengan garis l. Tentukan gradien garis l !

Penyelesaian :

Karena garis l sejajar dengan garis g, maka ml = mg = -5/3

Contoh 4 :

Garis k yang bergradien 2/5 tegak lurus dengan garis l. Tentukan gradien garis l !

Penyelesaian :

Karena garis l sejajar dengan garis k, maka ml X mk = -1 <=> ml = -1/mk = -5/2

Contoh 5 :

Tentukan gradien dari garis berikut :
1. 6x + 4y = 12
2. 3x - 8y + 15 =0

Penyelesaian :

1. 6x + 4y = 12 => m = -a/b = -6/4 = -3/2
2. 3x - 8y + 15 = 0 => m = -a/b = -3/(-8) = 3/8